Linear Regression using Gradient Descent

In this tutorial you can learn how the gradient descent algorithm works and implement it from scratch in python. First we look at what linear regression is, then we define the loss function. We learn how the gradient descent algorithm works and finally we will implement it on a given data set and make predictions.

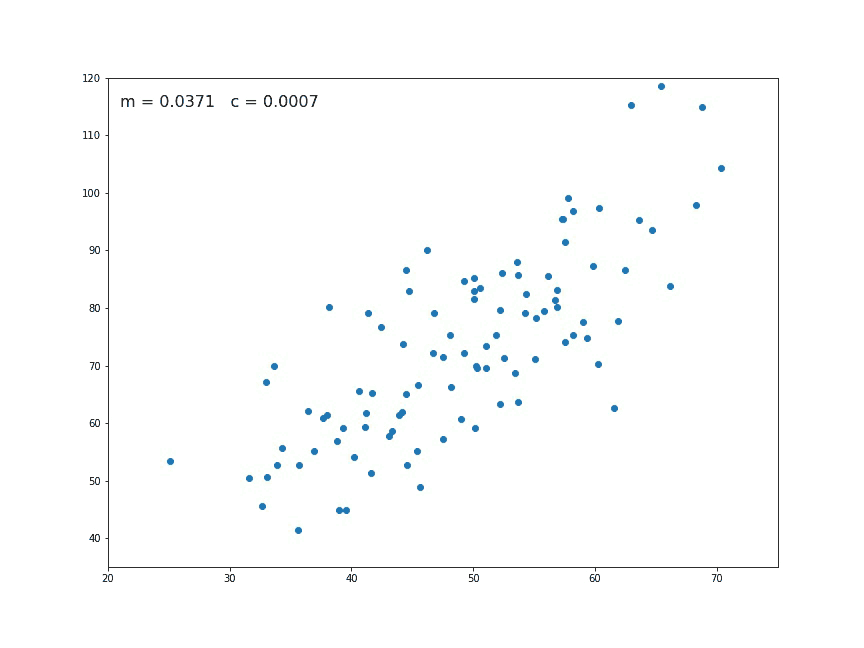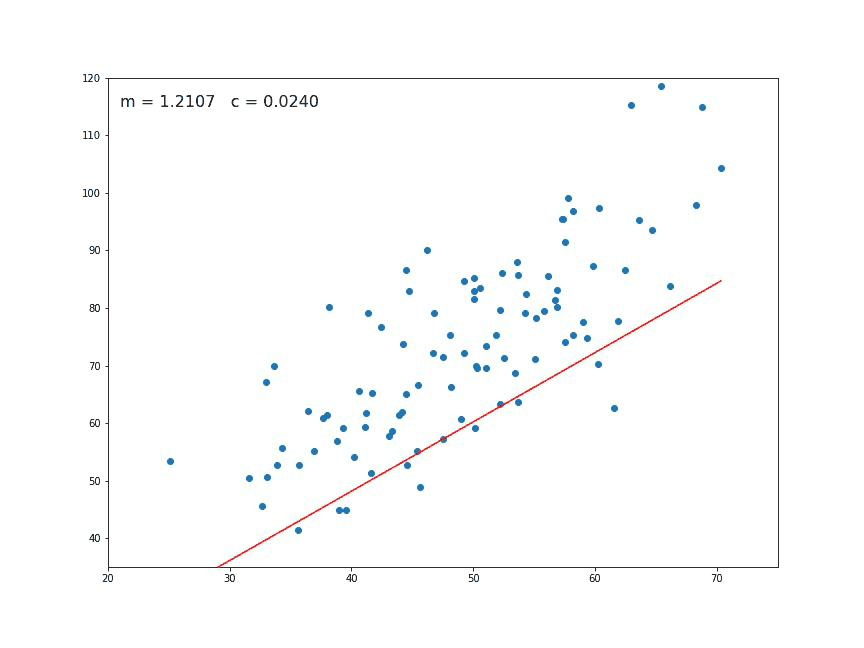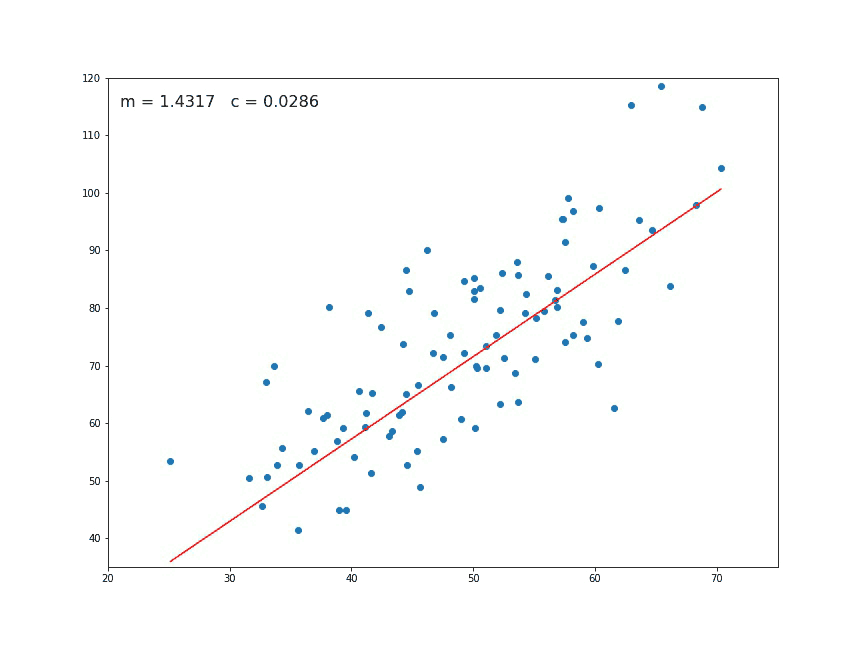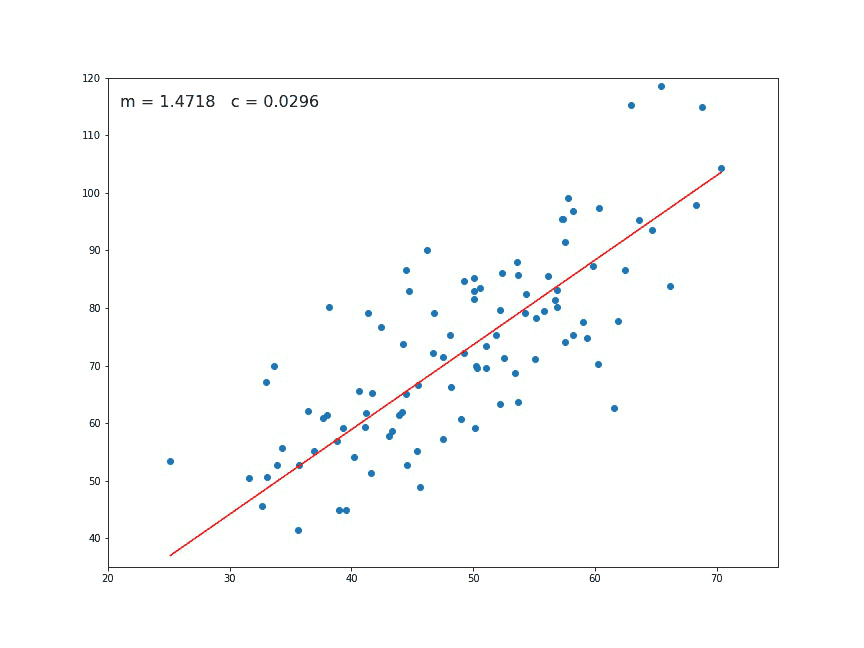
The values of m and c are updated at each iteration to get the optimal solution

Linear Regression

In statistics, linear regression is a linear approach to modelling the relationship between a dependent variable and one or more independent variables. Let X be the independent variable and Y be the dependent variable. We will define a linear relationship between these two variables as follows:

Source: http://www.nabla.hr/SlopeInterceptLineEqu.gif

This is the equation for a line that you studied in high school. m is the slope of the line and c is the y intercept. Today we will use this equation to train our model with a given dataset and predict the value of Y for any given value of X. Our challenge today is to determine the value of m and c, such that the line corresponding to those values is the best fitting line or gives the minimum error.

Loss Function

The loss is the error in our predicted value of m and c. Our goal is to minimize this error to obtain the most accurate value of m and c. We will use the Mean Squared Error function to calculate the loss. There are three steps in this function:

1. Find the difference between the actual y and predicted y value(y = mx + c), for a given x.
2. Square this difference.
3. Find the mean of the squares for every value in X.

Mean Squared Error Equation

Here yᵢ is the actual value and ȳᵢ is the predicted value. Lets substitute the value of ȳᵢ:

Substituting the value of ȳᵢ

So we square the error and find the mean. hence the name Mean Squared Error. Now that we have defined the loss function, lets get into the interesting part — minimizing it and finding m and c.

The Gradient Descent Algorithm

Gradient descent is an iterative optimization algorithm to find the minimum of a function. Here that function is our Loss Function.

Understanding Gradient Descent

Illustration of how the gradient descent algorithm works

Imagine a valley and a person with no sense of direction who wants to get to the bottom of the valley. He goes down the slope and takes large steps when the slope is steep and small steps when the slope is less steep. He decides his next position based on his current position and stops when he gets to the bottom of the valley which was his goal.

Let’s try applying gradient descent to m and c and approach it step by step:

1. Initially let m = 0 and c = 0. Let L be our learning rate. This controls how much the value of m changes with each step. L could be a small value like 0.0001 for good accuracy.
2. Calculate the partial derivative of the loss function with respect to m, and plug in the current values of x, y, m and c in it to obtain the derivative value D.
   

   Derivative with respect to m

   Dₘ is the value of the partial derivative with respect to m. Similarly lets find the partial derivative with respect to c, Dc:
   

   Derivative with respect to c

3. Now we update the current value of m and c using the following equation:
   
4. We repeat this process until our loss function is a very small value or ideally 0 (which means 0 error or 100% accuracy). The value of mand c that we are left with now will be the optimum values.

Now going back to our analogy, m can be considered the current position of the person. D is equivalent to the steepness of the slope and L can be the speed with which he moves. Now the new value of m that we calculate using the above equation will be his next position, and L×Dwill be the size of the steps he will take. When the slope is more steep (D is more) he takes longer steps and when it is less steep (D is less), he takes smaller steps. Finally he arrives at the bottom of the valley which corresponds to our loss = 0.

Now with the optimum value of m and c our model is ready to make predictions !

Implementing the Model

Now let’s convert everything above into code and see our model in action!

1.4796491688889395 0.10148121494753726

Gradient descent is one of the simplest and widely used algorithms in machine learning, mainly because it can be applied to any function to optimize it. Learning it lays the foundation to mastering machine learning.

Find the data set and code here.